10271. АДА школа

В классе ADA School расположены n × m парт, образующих прямоугольную сетку из n строк и m столбцов. Каждая парта занята ровно одним учеником.

Перед началом занятия учитель решил немного перетасовать учеников. После перестановки должны быть выполнены два условия:

· Каждый стол снова должен быть занят ровно одним учеником.

· Каждый ученик должен пересесть за стол, примыкающий к его исходному месту, то есть расположенный непосредственно слева, справа, сверху или снизу.

Можно ли выполнить перестановку учеников, соблюдая оба условия?

Вход. Первая строка содержит количество тестов t. Каждая из следующих t строк содержит два целых числа n и m (2 ≤ n, m ≤ 1000).

Выход. Для каждого теста выведите “YES”, если перестановку учеников можно выполнить, и “NO” в противном случае.

Пример входа	Пример выхода
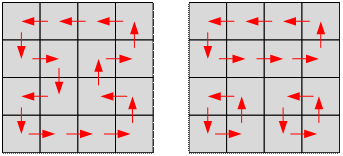
2 5 5 4 4	NO YES

РЕШЕНИЕ

математика

Анализ алгоритма

Рассмотрим случай, когда одна из размерностей сетки четная. Пусть, например, n (количество строк) – четное. В этом случае перестановку учеников можно выполнить следующим образом:

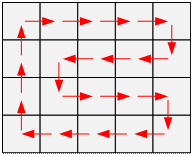
Если n и m нечётные, то выполнить перестановку невозможно.

Рассмотрим сетку, раскрашенную в шахматном порядке: одни клетки – белые, другие – чёрные. При перемещении парта, стоявшая на чёрной клетке, должна перейти на белую, и наоборот. Чтобы перестановка всех парт была возможна, количество белых и чёрных клеток должно быть одинаковым. Следовательно, общее число парт должно быть чётным.

Однако при нечётных n и m общее количество парт n × m является нечётным числом, что делает перестановку невозможной.

Реализация алгоритма

Читаем количество тестов t.

scanf("%d", &t);

while (t--)

{

Читаем входные данные каждого теста.

scanf("%d %d", &n, &m);

Если n и m нечетные, то выводим ответ “NO”.

if (n % 2 == 1 && m % 2 == 1)

puts("NO");

Иначе выводим ответ “YES”.

else

puts("YES");

}